Back to index

Mergable Priority Queues

• what if we wanted to merge two priority queues?
• normal min-heap implementation does not support this in a smart way
  • with min-heap data structure, must take all elements from both and construct new heap from scratch

Operations

• insert(A, x)
  • add an element x
• min(A)
  • return the highest priority element
• extract_min(A)
  • remove and return the highest priority element
• union(A, B)
  • create a new heap with all the elements of both A and B
• decrease_key(A, x, k)
  • decrease the key of x to k
• remove(A, x)
  • remove x from the heap entirely

Binomial Trees

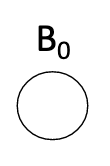
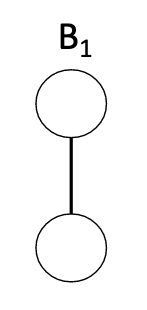
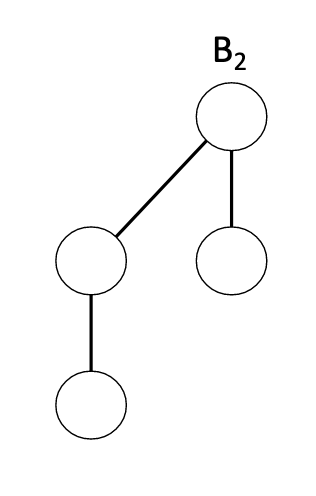
$B_k$ Trees defined recursively:

1. 
2. 
3. 

In general, create $B_{n+1}$ tree by taking two $B_n$ trees, $A$ and $B$ and making the root of $B$ the first child of the root of $A$

Properties of $B_k$

• number of nodes is $2^k$
• height of tree is $k$
• number of nodes with height $h$ is binomial coefficient $\displaystyle {k \choose h}$

Binomial Forest of size $n$ ($F_n$)

A sequence of $B_k$ trees with $k$ strictly decreasing with $n$ total nodes

• this is always possiblle because we can always represent $n > 0$ in binary, so we can always write it as a sum of unique powers of 2
• if $\alpha(n)$ is the number of 1s in the binary representation of $n$
  • $F_n$ has $\alpha(n)$ trees
  • $F_n$ has $n - \alpha(n)$ edges
  • $\alpha(n) \in \mathcal O(\log(n))$

Min Binomial Heap

A min binomial heap is a binomial forest where:

• each node of $F_n$ stores one element
• each tree in $F_n$ is min-heap ordered

Implementation

Storage

• edges as drawn are not exactly stored as pointers
• each node stores pointers to:
  • parent
  • left_child
  • right_sibling
• tree stores pointer to head, aka rightmost top level node

Merging min binomial heaps of same size $P_k$ and $Q_k$

• if Pk.root < Qk.root then make Pk.left_child = Qk.root, otherwise Qk.left_child = Pk.root
  • change parent pointers similarly

Union of min binomial forests (union(A, B))

(works exactly like algorithm for addition of binary numbers)

1. start at smallest $B_k$ tree in both
2. if tree is only in one forest (or is carry), then keep as-is in the union forest
3. if there are $B_k$ trees with same size in both, merge them to get a $B_{k+1}$ tree
4. carry the new $B_{k+1}$ tree, repeat from step 2

for $\vert A \vert \leq n$ and $\vert B \vert \leq n$, the complexity of union(A, B) is $\mathcal O(\log(n))$

insert(A, x)

Make a new binomial forest with a single $B_0$ tree which stores x, then “add” it to A

def insert(A, x):
    b = new B_0 Tree
    b.insert(x)
    B = new BinomialHeap(b)
    A = union(A, B)

decrease_key(A, x, k)